 A LEVEL COMPUTING
A LEVEL COMPUTING Data Structures
Data Structures Theory
Theory
16. The BINARY SEARCH TREE
One of the most powerful uses of the TREE data structure is to sort and manipulate data items.
Most databases use the Tree concept as the basis of storing, searching and sorting its records.
The Binary search tree holds data items in a sorted order, but with the addition of a simple rule
Rule: The LEFT node always contain values that come before the root node and the RIGHT node always contain values that come after the root node.
For numbers, this means the left sub-tree contains numbers less than the root and the right sub-tree contains numbers greater than the root. For words, as might be in a sorted dictionary, the order is alphabetic.
Example - forming a binary search tree.
A sequence of numbers are to formed into a binary search tree. These numbers are available in this order: 20, 17, 29, 22, 45, 9, 19. Task: form a sorted binary tree diagram
This is done step by step.
Sequence 20, 17, 29, 22, 45, 9, 19
1. The first item is 20 and this is the root node, so begin the diagram

2. Sequence 20, 17, 29, 22, 45, 9, 19
This is a binary search tree, so there are two child nodes available, the LEFT and the RIGHT. The next number is 17, the rule is applied (left is less than parent node) and so it has to be the LEFT node, like this

3. Sequence 20, 17, 29, 22, 45, 9, 19
The next number is 29, this is higher than the root node so it goes to the RIGHT sub-tree which happens to be empty at this stage, so the tree now looks like

4. Sequence 20, 17, 29, 22, 45, 9, 19
The next number is 22. This is more that the root and so need so be on the RIGHT sub-tree. The first node is already occupied. So the rule is applied again to that node, 22 comes before 29 and so it needs to be on the LEFT sub-tree of that node, like this
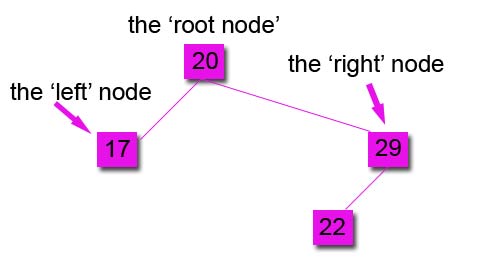
5. Sequence 20, 17, 29, 22, 45, 9, 19
The next number is 45, this is more than the root and more than the first right node, so it is placed on the right side of the tree like this
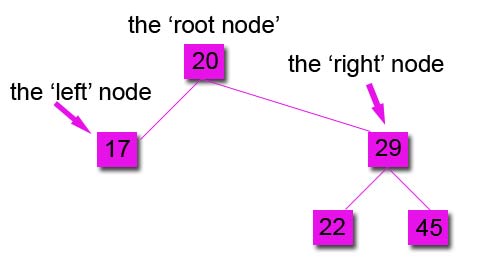
6. Sequence 20, 17, 29, 22, 45, 9, 19
The next number is 9 which is less than the root, the first left node is occupied and 9 is less than that node too, so it is placed on the left sub-tree, like this
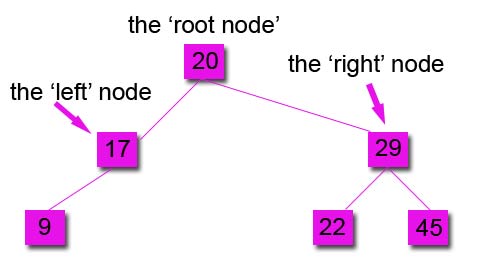
Step 7 Sequence 20, 17, 29, 22, 45, 9, 19
The next number is 19, which is less than the root, so it will need to be in the left sub-tree. It is greater than the occupied 17 node and so it is placed in the right sub-tree, like this
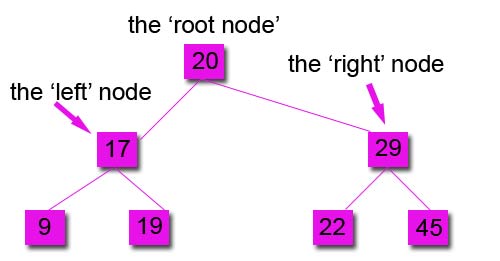
The tree is now complete.
Copyright © www.teach-ict.com

