10. Normalised Floating point

We want the floating point system to represent as wide a range of real numbers with as much precision as possible.

Don't forget, only a fixed number of bits are available in any given scheme (8 bit, 16 bit, 32 bit, 64 bit and so on).

For example, say you want to use an 8 bit scheme. Say, 3 bits for the exponent, 1 bit for the sign, 3 bits for numbers greater than 1 which only leaves 1 bit for a fraction. Like this

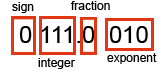
The largest number this can represent is 111.1 with a 111 exponent which is 7.5 x 2^7, but fractionally you can only represent 0.5 any other fraction is not possible because you have only provided 1 bit in this scheme. So this scheme is pretty hopeless in terms of precision.

So let's swap around the scheme slightly. This time we only allow 1 bit for the integer and 3 bits for the fractional part. Like this

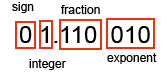
This time you have three fractional bits to use so any combination of 1/2 , 1/4, 1/8 can be used to describe a number, whilst the integer part can only be a 1 or a zero. Now the largest number that can be represented is 1.111 x 2^7 which is not that much less than the 7.5 x 2^7 above. And yet we can now represent 0.001 binary which is 1/8. A good improvement in precision.

If we want to represent say 6.0 then you use the exponent to move the binary point, like this

0 1.100 010

expand this out by moving the binary point by the exponent and you get 110.0 which is 6.0 decimal.

This trick of only allowing 1 bit for the integer part of a real number is called 'Normalisation'

Normalisation means that except for zero, a real number is represented with 1 integer and a fractional part like this 1.fff

This scheme sacrifices a bit of range but gains significantly in precision.

Tip: Spotting a normalised number.

Which of these are normalised numbers (8 bit scheme, 3 bit exponent, uses twos complement)

1. 00110 011
2. 01100 010

Answer: If the left 2 bits change sign, then that indicates the number is normalised.

In the example above, they can both represent 3 decimal. But the first one is not normalised but the second one is normalised.

In the first example the binary number is 0.0110 and the exponent is 3 so move the binary point three places to the right. You get 11.0 which is 3 decimal

In the second example the binary number is 0.1100 with the exponent 2 so move the binary point two places to the right and you still get 11.00 which is once again 3 decimal. But note that you now have 2 binary bits after the point, which indicates you have more precision available.