3. Karnaugh map grid
From the previous page, this is the expression we want to simplify
$$Q = \overline A. \overline B.C. \overline D + \overline A. \overline B.C.D + \overline A.B.C. \overline D + \overline A.B.C.D + A. \overline B. \overline C. \overline D + A.B. \overline C. \overline D + A.B. \overline C.D $$
This is done with the following steps:
- Create a grid for the karnaugh map
- Fill in the '1's in the appropriate places
- Split the map up into regions
- Create minterms for each region
- Combine the minterms
Step 1: Creating the grid
Karnaugh maps are two-dimensional. So with four inputs, the first step is to combine them together to fit onto two axes. We'll pair up A and B to produce AB for one axis. And we'll pair C and D to produce CD for the other axis.
The next step is to label each row and column. A can only be 0 or 1, and B can only be 0 or 1, so there are four possible values for AB - 00, 01, 10, and 11. The same is true for the pair CD.
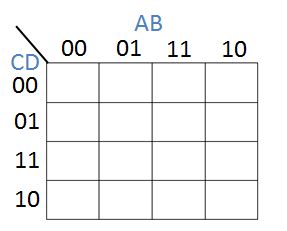
An important thing to notice is the sequence of AB (same for CD) - only one bit it allowed to change as you go from one state to another. For example this sequence is NOT correct: 00,01,10,11 because two bits changed to go from 01 to 10. A binary sequence where only one bit changes along the sequence is called a gray code after Frank Gray. Karnaugh maps use gray code to determine the rows and columns.
So what do these cells actually represent? Let's look at the top left cell:
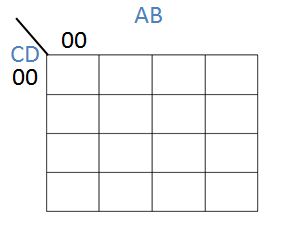
In this cell, the result is not-A AND not-B AND not-C AND not-D. Or, in Boolean algebra, $\overline A. \overline B. \overline C. \overline D$, with a top bar representing NOT and a dot representing the AND operator.
The next pair of cells represent expressions with a single True value - either B or D:
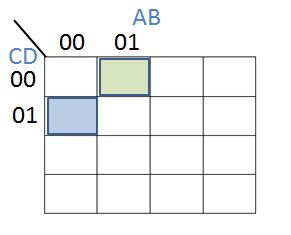
The green cell represents $\overline A. B. \overline C. \overline D$ and the blue cell represents $\overline A. \overline B. \overline C.D$
Next, place a 11 alongside:
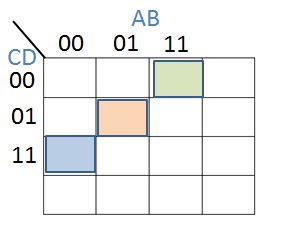
The green cell is $A.B. \overline C. \overline D$, the orange cell is $\overline A.B. \overline C.D$ and the blue cell is $\overline A. \overline B.C.D$
Now finally place a 10 next to the 11:

This is the empty four-variable karnaugh map. Because there are 16 cells, every possible combination of $A,B,C,D$ can be defined.
It is important to note that this is a representation of logic, rather than binary arithmetic. Unlike binary arithmetic, where 00 and 10 represent 0 and 2 the sequence 00 means two inputs with each at state 0.
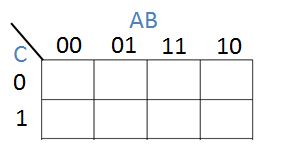
An empty karnaugh map for three variables would look like this:
Challenge see if you can find out one extra fact on this topic that we haven't already told you
Click on this link: Karnaugh Map rules
