3. Floating point
The alternative to fixing the decimal point/binary point at a single position is to let it "float" back and forth as needed. This is called a floating point number system.
Floating point can be used to represent a wider range of real numbers in a limited number of bits, compared to the fixed point approach.
Floating point is similar to representing a number in scientific notation :-
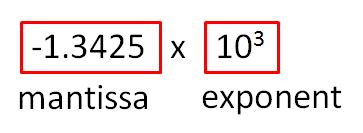
The 'mantissa' holds the number value and its sign and the 'exponent' defines where the decimal point needs to be if the number is shown in standard format. In the above case, the $10^3$ indicates that it needs to be multiplied by a thousand and so the radix point has to move three places to the right, like this :
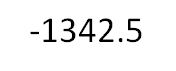
Binary floating point uses the same idea. A binary floating point number is in two parts. The Mantissa and the Exponent. Here is an 8 bit floating point number

The mantissa and the exponent are treated as separate numbers in two's complement. That is, each uses the leftmost digit (most significant bit or MSB) to express whether they're positive or negative.
If there is a 1 present in the MSB of the mantissa then it is a negative number. If there is a 1 in the MSB in the exponent then it is a negative exponent (in decimal this is like $10^{-3}$.)

We continue on the next page
