3. Normalised floating point
We want the floating point system to represent as wide a range of real numbers with as much precision as possible.
Normalisation means that except for zero, a real number is represented with one integer and a fractional part like this 1.fff . A normalised floating point number has the most precision.
For example, you want to use an 8 bit scheme with 3 bits for the exponent, 1 bit for the sign, 3 bits for numbers greater than 1 which only leaves 1 bit for a fraction. Like this
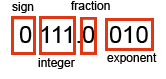
The largest number this can represent is 111.1 with a 111 exponent which is 7.5 x 27, but fractionally you can only represent 0 or 1/2 any other fraction is not possible because you have only provided 1 bit in this scheme. So this scheme is pretty hopeless in terms of precision.
Let's swap around the scheme slightly. This time we only allow 1 bit for the integer and 3 bits for the fractional part. Like this
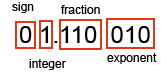
This time you have three fractional bits to use so any combination of 1/2 , 1/4, 1/8 can be used to describe a number, whilst the integer part can only be a 1 or a zero. Now the largest number that can be represented is 1.111 x 27 which is not that much less than the 7.5 x 27 above. And yet we can now represent 0.001 binary which is 1/8. A good improvement in precision.
This trick of only allowing 1 bit for the integer part of a real number is called 'Normalisation'
This scheme sacrifices a bit of range but gains significantly in precision.
Challenge see if you can find out one extra fact on this topic that we haven't already told you
Click on this link: Floating point precision
